Chapitre 3 : Opérations sur les nombres binaires dans le microprocesseur
3.1 Introduction
Dans un ordinateur, les opérations arithmétiques s'effectuent en 8 bits, 16 bits, 32 bits ou 64 bits. Un nombre comme 3 en binaire vaut 11. Si l'opération doit être effectuée sur 8 bits, cela est considéré comme 00000011 ; le précédant de 0 zéros.
Pour un nombre binaire comme 10000101, le bit le plus significatif est celui situé à l’extrême gauche. C'est 1 dans ce cas. Le bit le moins significatif est le bit extrême à droite, qui est toujours 1, pour le nombre. Le bit le plus significatif est abrégé en MSB. Le bit le moins significatif est abrégé en LSB.
Le chiffre BInary est abrégé en BIT et s'écrit simplement en bit. Dans le nombre 10010011, chaque un ou zéro est un bit. Un groupe de quatre bits est appelé un quartet. Un groupe de huit bits est appelé un octet. Un octet est constitué de deux quartets. Le quartet inférieur est le quartet pour le LSB et le quartet supérieur est le quartet pour le MSB.
Un groupe de 8 bits, 16 bits, 32 bits ou 64 bits est appelé un mot, tant que ce groupe transmet des informations au-delà de la simple indication d'un nombre. Le groupe est appelé mot, par exemple, s'il s'agit d'une instruction de bas niveau dans l'ordinateur. Il existe également un mot de 24 bits, mais celui-ci n'est pas couramment utilisé aujourd'hui.
L'endianité fait référence à l'ordre dans lequel les octets forment un mot. Considérons le mot de 24 bits – 100100001111010100100010. Ce mot se compose de trois octets qui sont :
10010000 11110101 00100010
L'octet de poids fort est l'octet le plus à gauche. Lorsque l'octet à l'extrême gauche est l'octet de poids fort et que l'octet à l'extrême droite est l'octet de poids faible, on parle alors de représentation Big Endian du mot. La représentation Little Endian est à l’opposé.
La mémoire de l’ordinateur est une série de cellules et chaque cellule contient un octet. La première cellule de la mémoire de l’ordinateur correspond à l’octet 0, la seconde à l’octet 1, la troisième à l’octet 2, et ainsi de suite. Avec le big endianness et pour le mot précédent, l'octet de poids fort est stocké dans la cellule d'octet 0, l'octet du milieu est stocké dans la cellule d'octet 1 et l'octet de poids faible est stocké dans la cellule d'octet 2. Cela signifie qu'il y a des octets plus significatifs dans la cellule mémoire inférieure.
Le mot précédent de 24 bits peut être écrit dans l'ordre inverse des octets comme suit :
00100010 11110101 10010000
Désormais, l’octet de poids faible se trouve à l’extrême gauche et l’octet de poids fort à l’extrême droite. Lorsque l'octet à l'extrême gauche est l'octet de poids faible et que l'octet à l'extrême droite est l'octet de poids fort, il s'agit de la représentation Little Endian du mot. Avec peu d'endianisme et pour le mot précédent, l'octet de poids faible est stocké dans la cellule d'octet 0, l'octet du milieu est stocké dans la cellule d'octet 1 et l'octet de poids fort est stocké dans la cellule d'octet 2. Cela signifie qu'il y a un octet moins significatif dans la cellule mémoire inférieure.
L'endianité n'est pas utilisée pour les bits d'un octet. Il n’est pas non plus utilisé pour les quartets dans un octet. Il n'est utilisé que pour l'ordre des octets.
La droite numérique
Un nombre sans signe est un nombre positif. Les nombres positifs sont des nombres partant de zéro et allant vers le haut. Des nombres négatifs existent également. Les nombres positifs et négatifs peuvent être présentés sur une droite numérique. La droite numérique suivante montre les nombres entiers positifs et négatifs (entiers) proches de zéro :
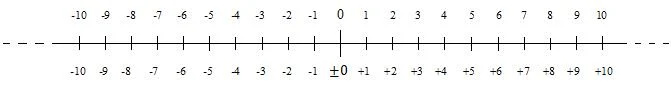
Les nombres négatifs diminuent de zéro vers le bas (vers la gauche). Dans de nombreuses situations, zéro est considéré comme positif. Cependant, elle est considérée comme négative dans certaines situations. C'est pourquoi il y a un signe plus et moins devant zéro, dans la numérotation inférieure du diagramme. Lorsqu'un nombre est positif, son signe peut être omis ; c'est le cas de la numérotation supérieure du diagramme. Le signe moins devant un nombre négatif n’est jamais omis.
3.2 Ajout de nombres binaires
En plus :
A + B = S
A est appelé l'augend, B est appelé l'addition et S est appelé la somme.
Considérons l’addition suivante de deux nombres positifs en base deux :

En base deux, les seuls chiffres possibles sont 0 et 1. L'addition en base 2 est similaire à l'addition en base dix, mais deux en base deux valent un-zéro (10). Lorsque la somme de deux bits dans une colonne est 10, 0 est écrit et 1 est reporté dans la colonne de gauche immédiate ; à ajouter à la somme des deux bits. Lorsque la somme totale est de trois, cela signifie 11 en base deux. Le 1 de droite sur 11 est écrit et le 1 de gauche est porté pour être ajouté à la somme des bits immédiats de la colonne de gauche. Dans les deux cas, le 1 porté vers la gauche est appelé le carry.
En lisant le tableau d'addition précédent par la droite, dans la deuxième colonne (en partant de la droite), on a une retenue qui résulte de 1+1 = 10. Dans la troisième colonne, on a une retenue qui résulte de 1+1+ retenue de 1 = 11. Dans la quatrième colonne, il y a un report qui résulte de 0+1+ report de 1 = 10. Dans la cinquième colonne, il n'y a pas de report car la sommation est 0+0+ report de 1 = 1. Le le reste des colonnes n’implique aucun report.
Le comptage des colonnes commence par l'extrémité droite. Avec une addition de 16 bits, il peut y avoir un report de la huitième colonne à la neuvième colonne (en se déplaçant vers la gauche). Le tableau suivant illustre ceci :

Les opérations arithmétiques et logiques ont lieu dans le microprocesseur de la carte mère de l'ordinateur.
Pour un ordinateur de mots de 8 bits, le report ne peut pas passer automatiquement du huitième bit au neuvième bit automatiquement par le matériel. Ainsi, pour ajouter deux groupes de 16 bits dans un tel ordinateur, l'addition doit être effectuée deux fois par paires de huit à huit bits. Le report est déplacé et effectué par le logiciel (programmation).
Pour additionner deux nombres, les nombres peuvent d’abord être convertis sous leur forme de complément à deux (voir ci-dessous) avant de les additionner.
3.3 Le complément à deux et sa soustraction de nombres binaires
Sur la carte mère de l’ordinateur, il y a la mémoire et il y a le microprocesseur et d’autres circuits. La mémoire est une série de cellules de huit bits. Pour un octet, chaque bit va dans une cellule. Le microprocesseur possède quelques emplacements de type mémoire. Ces emplacements de type mémoire sont appelés registres. Ainsi, dans l'ordinateur, des groupes d'octets peuvent être stockés temporairement dans la mémoire ou dans les registres du microprocesseur.
Dans n’importe lequel de ces stockages, chaque cellule peut prendre soit un 1, soit un 0, et rien d’autre. Dans la vie, il y a des nombres positifs et négatifs. Un nombre positif commence par un signe plus (+) et un nombre négatif commence par un signe négatif (-). Lorsque le signe est omis, le nombre est considéré comme un nombre positif.
Afin de résoudre ce problème d'indication du signe d'un nombre dans l'ordinateur, les nombres entiers sont stockés dans des plages. Les nombres entiers sont des entiers. Si huit bits sont utilisés pour stocker la plage de nombres possibles, le bit le plus à gauche est utilisé comme bit de signe. Si le nombre commence par 0, le nombre est un nombre positif. S’il commence par 1, le nombre est un nombre négatif. Si seize bits sont utilisés pour stocker la plage de nombres possibles, le bit le plus à gauche est utilisé comme bit de signe. Si le nombre commence par 0, le nombre est un nombre positif. S’il commence par 1, le nombre est un nombre négatif. Les nombres sous cette forme sont appelés nombres signés.
En pratique, il peut y avoir des nombres signés pour 8 bits, 16 bits, 32 bits et 64 bits. Plus le nombre de bits utilisés est large, plus la plage de nombres possibles pouvant être stockés est grande.
Entiers complémentaires à deux
Avec le complément à deux, les nombres positifs sont les nombres de comptage normaux, sauf que le chiffre le plus à gauche est 0. Pour obtenir le nombre négatif correspondant à tout nombre positif donné, inversez chaque bit du nombre et ajoutez 1 au résultat. L’inverse ou le complément de 0 est 1. L’inverse ou le complément de 1 est 0. Les tableaux suivants montrent quelques nombres complémentaires à deux dans leurs plages :
| Tableau 3.31 Complément à deux d'entiers sur deux bits |
|
|---|---|
| Binaire | Décimal |
| 01 | +1 |
| 00 | +0 |
| onze | -1 |
| dix | -2 |
Les nombres binaires positifs sont 00 et 01 (soit zéro et un). Dans le bit le plus à gauche, zéro indique qu’il s’agit de nombres positifs. 00 se situe quelque peu au milieu de la fourchette. Pour obtenir -1, l'inverse du nombre 01 est 10. En y ajoutant 1 (à l'extrême droite), on obtient 11.
Puisque deux bits sont utilisés, il ne reste qu'un seul bit pour représenter les nombres dans la plage composée des nombres +1, +0 et -1 correspondant à 01, 00 et 11. Le premier bit indique le signe. Il arrive que 10 pour +2 ne fasse pas partie de ces trois nombres binaires. 10 commence par 1, ce qui signifie qu’il doit être un nombre négatif en complément à deux. Ainsi, 10 est inclus dans la plage, ce qui signifie -2.
Avec deux bits en complément à deux, le nombre de tous les entiers (positifs et négatifs) pouvant être représentés est 2 2 = 4 et non 2 2 -1 = 3. La nuance résulte de l'inclusion du dernier nombre négatif qui est le négatif de 2 numéroavec – 1. Dans ce cas, -2 2-1 = -2 1 = -2. Il n’y a pas de +2 dans l’intervalle des nombres complémentaires à deux sur 2 bits.
| Tableau 3.32 Complément à deux d'entiers sur quatre bits |
|
|---|---|
| Binaire | Décimal |
| 0111 | +7 |
| 0110 | +6 |
| 0101 | +5 |
| 0100 | +4 |
| 0011 | +3 |
| 0010 | +2 |
| 0001 | +1 |
| 0000 | +0 |
| 1111 | -1 |
| 1110 | 1110 |
| 1101 | -3 |
| 1101 | -3 |
| 1100 | -4 |
| 1011 | -5 |
| 1010 | -6 |
| 1001 | 1001 |
| 1000 | -8 |
Les nombres binaires positifs vont de 0000 à 0111 (soit de zéro à sept). Dans le bit le plus à gauche, zéro indique qu’il s’agit de nombres positifs. 0000 se situe quelque peu au milieu de la fourchette. Pour obtenir -1, l'inverse du nombre 0001 est 1110. En y ajoutant 1 (à l'extrême droite), on obtient 1111. Pour obtenir -2, l'inverse de 0010 est 1101. En ajoutant 1 à cela ( à partir de l'extrême droite) donne 1110. Les autres nombres binaires négatifs comme -3 à -7 sont déterminés de la même manière.
Puisque quatre bits sont utilisés, il reste trois bits pour représenter les nombres dans la plage qui sont +7, +6, +5, +4, +3, +2, +1, +0, -1, -2, - 3, -4, -5, -6 et -7 correspondant à 0111, 0110, 0101, 0100, 0011, 0010, 0001, 0000, 1111, 1110, 1101, 1100, 1011, 1010 et 1001.
Le -8 qui correspond à 1000 doit être traité séparément. Le premier bit de tous ces nombres indique le signe 0 pour les nombres positifs et 1 pour les nombres négatifs. Il arrive que 1000 ne fasse pas partie de ces quatorze nombres binaires. 1000 commence par 1, ce qui signifie qu’il doit être un nombre négatif en ce qui concerne le complément à deux. Ainsi, 1000 est inclus dans la plage, ce qui signifie -8.
Avec quatre bits en complément à deux, le nombre de tous les entiers (positifs et négatifs) pouvant être représentés est 2 4 = 16 et non 2 4 – 1 = 15. La nuance résulte de l’inclusion du dernier nombre négatif qui est le négatif de 2 nombreLargeur – 1. Dans ce cas, -2 4 -1 = -2 3 = -8. Il n’y a pas de +8 dans la plage de nombres.
L’analyse précédente pour les bits de deux, quatre et plus larges en complément à deux peut être appliquée aux nombres binaires de 8 bits, 16 bits, 32 bits et 64 bits de large.
Le complément à deux sacrifie le premier bit (le plus à gauche) pour le signe 0 pour un nombre positif et 1 pour un nombre négatif. Pour le groupe de bits de largeur « n » bits, il y a 2 n nombres totaux positifs et négatifs. Ce serait 2 n -1, sans le dernier (plus petit) nombre négatif chanceux inclus. Le nombre positif le plus élevé est +2 n-1 -1 et le plus petit nombre négatif est -2 n-1 -1. ce serait -2 n-1 -1, n'était-ce pas pour les chanceux -2 n-1 inclus.
Soustraire des nombres en complément à deux
En soustraction :
A – B = D
A est appelé le menu, B est appelé le sous-trahend et D est appelé la différence.
Pour soustraire un nombre binaire positif d’un autre nombre binaire positif, la fin du minuend est écrite en complément à deux et la soustrahend est convertie en sa valeur de complément à deux négatif. Ainsi, l’énoncé mathématique devient :
A+ – B = D
En d’autres termes, dans la soustraction du complément à deux, le soustrahend est converti en un nombre négatif puis ajouté au minuend.
Exemple 3.31 :
Évaluez l’expression décimale suivante en complément à deux en utilisant quatre bits :
6 – 4
Solution:
Le nombre binaire pour 6 est 110. En complément à deux de 4 bits, c'est 0110. Le nombre binaire pour +4 est 100. En complément à deux de 4 bits, c'est 0100. 0100 qui doit être converti en moins 4 en deux. compléter comme suit : Le complément ou l'inversion de 0100 est 1011. En y ajoutant 1 à partir de l'extrémité droite, comme nous l'avons fait en plus, nous obtenons 1100. Ainsi, l'expression décimale est :
6 – 4 qui devient :
0110 – 0100 qui est
0110 +(– 0100) = 0110 + 1100 fait comme dans la section d'addition précédente comme :

Remarque : 0110 + (– 0100) est identique à 6 + – 4
Avec la soustraction du complément à deux, toute retenue, après la dernière colonne vers la gauche, dans l'addition, est supprimée. Lors d’une soustraction en décimal, l’énoncé mathématique est :
6 – 4 = 2
En faisant la même chose en complément à deux, la réponse est 0010, ce qui correspond à +2 en comptage binaire en complément à deux. La soustraction précédente soustrait un nombre plus petit à un nombre plus grand. Dans l’exemple suivant, un nombre plus grand est soustrait d’un nombre plus petit. Le tableau 3.32 peut être consulté pour voir si 0010 est bien le complément à deux qui équivaut à +2.
Exemple 3.32 :
Évaluez l’expression décimale suivante en complément à deux avec quatre bits :
4 – 6
Solution:
Le nombre binaire pour 4 est 100. En complément à deux de 4 bits, il est 0100. Le nombre binaire pour +6 est 110. En complément à deux de 4 bits, il est 0110. 0110 doit être converti en moins 6 en complément à deux. comme suit : Le complément ou l'inversion de 0110 est 1001. En y ajoutant 1 à partir de l'extrémité droite, comme nous l'avons fait lors de l'ajout précédent, nous obtenons 1010. Ainsi, l'expression décimale est :
4 – 6 qui devient :
0100 – 0110 qui est
0100 +(– 0110) = 0100 + 1010 fait comme dans la section d'addition précédente comme :

Remarque : 4+ – 6 équivaut à 0100 + (– 0110).
Avec la soustraction du complément à deux, toute retenue, après la dernière colonne vers la gauche, dans l'addition, est supprimée. Lors d’une soustraction en décimal, l’énoncé mathématique est :
4 – 6 = -2
En faisant la même chose en complément à deux, la réponse est 1110, soit -2 en comptage binaire en complément à deux. Le tableau 3.32 peut être consulté pour voir si 1110 est bien le complément à deux qui équivaut à -2.
3.4 Multiplication de nombres binaires
Dans la déclaration :
A x B = P
A est appelé multiplicande, B est appelé multiplicateur et P est appelé produit. L'expression A x B signifie ajouter A, B un certain nombre de fois lorsque A et B sont des nombres entiers (nombres entiers).
La multiplication en binaire est la même que la multiplication en décimal. Cependant, au lieu de le faire en décimal, cela se fait en binaire. La multiplication de l'expression décimale de 42 x 10 se fait en binaire comme suit où 42 dix = 101010 2 et 10 dix = 1010 2 :
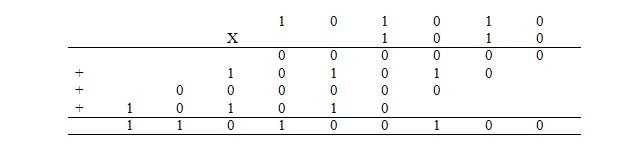
Les 4 nombres ajoutés sont appelés produits partiels. La réponse est le produit. L'ajout des produits partiels se fait de la même manière qu'expliqué précédemment.
La multiplication peut également être vue comme suit : Dans cette multiplication en base deux, si le bit (chiffre) du multiplicateur est 1, le bit de poids faible de son produit partiel est le bit de poids faible du multiplicande qui est retapé directement en dessous de lui ; et le reste des bits du multiplicande est répété vers la gauche. Dans cette multiplication en base deux, si le bit (chiffre) du multiplicateur est 0, son produit partiel est constitué de 0 avec le bit le moins significatif de 0 directement en dessous. Le nombre de zéros est le nombre de bits du multiplicande.
3.5 Division des nombres binaires
Dans la déclaration :
UNE ÷ B = Q
A est appelé le dividende, B est appelé le diviseur et P est appelé le quotient. Le quotient peut être accompagné d'un reste. L'expression A ÷ B signifie combien de fois B peut être ajouté pour donner A ou en être proche de telle sorte que le reste soit 0 ou inférieur à B.
La division peut se faire de plusieurs manières. La division représentée ici est la division de restauration.
Division en restauration
Il s’agit de la méthode de division longue qui s’apprend dans les écoles. Si 237 est divisé par 6, la réponse est 39 reste 3. Le 237 dix en base 2 est 11101101 2 et 6 dix en base 2 vaut 110 2 . Le 39 dix en base 2 est 100111 2 et 3 dix en base 2 vaut 11 2 .
Alors, 11101101 2 divisé par 110 2 donne 100111 2 reste 11 2 en base deux. Avec la méthode de restauration, les nombres binaires sont des nombres ordinaires et ils ne sont pas nécessairement en complément à deux. La structure suivante divise 11101101 2 par 110 2 donner 100111 2 reste 11 2 :

La soustraction se fait habituellement et non en utilisant le complément à deux. Puisqu’il s’agit de la base deux, un emprunt vaut deux et non dix. Les dividendes partiels sont 10, 101, 1011, 1010 et 1001. 11 est le reste. Puisque le diviseur comporte trois chiffres, la division se fait essentiellement par groupes de trois chiffres à partir du dividende donné. Le quotient est un nombre entier (entier), et c'est 100111 pour ce problème. Le résultat du quotient et du reste est comme prévu.
3.6 Opérations arithmétiques avec logiciel et matériel
La carte mère de l'ordinateur possède une horloge. Les tics de l'horloge sont appelés impulsions. A chaque impulsion d'horloge, une ou plusieurs décisions sont prises à différents endroits de la carte mère ; et cela a à voir avec la programmation (logiciel).
À l’intérieur du microprocesseur, il existe deux types de circuits appelés : circuits logiques combinatoires et circuits logiques séquentiels. Il existe un autre type de circuit appelé multiplexeur. L'addition, la multiplication et la division peuvent avoir lieu dans un intervalle d'horloge en utilisant la logique combinatoire (circuit). Tandis que la programmation (logiciel) engage la décision à chaque impulsion d'horloge en utilisant les circuits logiques séquentiels et les multiplexeurs.
Lorsque la soustraction est effectuée en complément à deux, au moins deux impulsions d’horloge sont nécessaires. À la première impulsion d'horloge, un multiplexeur canalise le sous-trahend vers un ensemble de portes NON (une porte NON par chiffre). À la deuxième impulsion d'horloge, la logique combinatoire ajoute 1 à la sortie des portes NON et continue d'ajouter le sous-trahend et le minuend résultants. Tout cet ajout peut avoir lieu dans un intervalle d’horloge.
L'addition, la multiplication et la division peuvent toujours échouer avec la programmation utilisant les tables de vérité. Cependant, cela n’est pas abordé dans ce cours de carrière en ligne.
3.7 Opérations logiques dans le microprocesseur
ET, OU, XOR et Inverser
ET
Le tableau suivant illustre le ET au niveau du bit. Cela signifie que pour deux nombres binaires différents, les bits correspondants sont traités par AND en fonction de la table AND Truth :
En allant de gauche à droite, 1 ET 1 = 1 ; 0 ET 1 = 0 ; 0 ET 0 = 0 ; 1 ET 0 = 0 ; et ainsi de suite conformément à la table de vérité AND.
OU
Le tableau suivant illustre le OU au niveau du bit. Cela signifie que pour deux nombres binaires différents, les bits correspondants sont combinés par OU en fonction de la table OR Truth :

En allant de gauche à droite, 1 OU 1 = 1 ; 0 OU 1 = 1 ; 0 OU 0 = 0 ; 1 OU 0 = 1 ; et ainsi de suite conformément à la table de vérité OR.
GRATUIT
Le tableau suivant illustre le OU exclusif au niveau du bit. Cela signifie que pour deux nombres binaires différents, les bits correspondants sont XORés sur la base de la table XOR Truth :

En allant de gauche à droite, 1 XOR 1 = 0 ; 0 XOR 1 = 1 ; 0 XOR 0 = 0 ; 1 XOR 0 = 1 ; et ainsi de suite conformément à la table de vérité XOR.
Inverser (PAS)
Le tableau suivant illustre le NOT au niveau du bit (inversion). Cela signifie que pour un nombre binaire, cette fois, chaque bit est inversé en fonction de la table de vérité NON :

En allant de gauche à droite, NOT 1 = 0 ; PAS 0 = 1 ; PAS 0 = 1 ; PAS 1 = 0 ; et ainsi de suite conformément à la table NOT Truth.
Déplacement vers la droite ou la gauche
Décaler vers la droite
Le nombre binaire suivant est décalé de 3 positions de bits vers la droite, les zéros étant insérés dans les positions de bits libérées à gauche :

Le déplacement peut se faire pour une, deux, trois, quatre places, etc.
Décaler vers la gauche
Le nombre binaire suivant est décalé de 3 positions de bits vers la gauche, les zéros étant insérés dans les positions de bits libérées à droite :

Le déplacement peut se faire pour une, deux, trois, quatre places, etc.
Rotation à droite ou à gauche
La rotation est similaire au déplacement. Cela se fait petit à petit. Lors d'une rotation à droite, les bits qui quittent l'extrémité droite ne tombent pas comme lors d'un déplacement ; ils remplacent les bits libérés sur la gauche, un par un. Lors d'une rotation à gauche, les bits qui quittent l'extrémité gauche ne tombent pas comme lors d'un déplacement ; ils remplacent les bits libérés à droite, un par un.
Tourner à droite
Le nombre binaire suivant subit une rotation de 3 bits vers la droite :

La rotation peut se faire pour une, deux, trois, quatre places, etc.
Rorate à gauche
Le nombre binaire suivant subit une rotation de 3 bits vers la gauche :

La rotation peut se faire pour une, deux, trois, quatre places, etc.
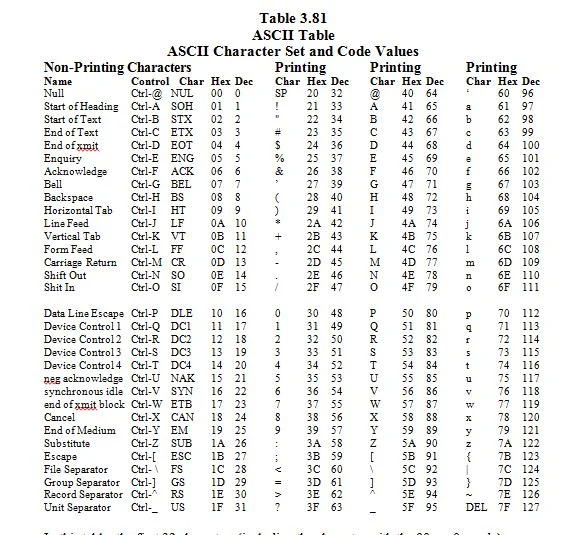
3.8 Jeu de caractères ASCII et ses valeurs de code
ASCII signifie « Code standard américain (États-Unis) pour l'échange d'informations ». Imaginez un clavier avec 96 touches. Il s’agit d’un clavier idéal où les touches des lettres majuscules sont différentes des touches des lettres minuscules. Une touche sur deux représente un caractère trouvé sur un clavier anglais (États-Unis). Les caractères et les codes (numéros correspondants aux caractères) sont répertoriés comme suit :
Dans ce tableau, les 32 premiers caractères (y compris le caractère avec le 00 16 = 0 dix code) sont des caractères non imprimables. Ce sont des personnages de contrôle. Ils ne sont pas vus sur l'écran (moniteur) où tout est égal. Ils n'ont que des effets. Discutons-en davantage plus tard.
Le reste des caractères sont des caractères imprimables ; ils sont vus à l'écran. Il y a 128 caractères ASCII. 2 7 = 128. 1 111 111 2 = 127 dix . Le 7 en 2 7 signifie 7 bits.
Maintenant, 1111111 2 + 1 2 est le même que:
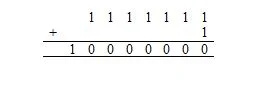
Ici, 10 000 000 2 = 128 dix . Il y a 128 dix caractères de la liste (tableau) précédente de caractères ASCII. Cela inclut le caractère nul, dont le code en base seize (hexadécimal) est 00, ce qui équivaut à 0 en base dix.
Puisqu'il y a 128 caractères au total, 128 moins 32 caractères non imprimables donnent 96 caractères imprimables. Dans cette section, on suppose qu’il existe un clavier idéal comportant 96 caractères imprimables. Sur ce clavier idéal, les touches des caractères anglais majuscules sont différentes des touches des caractères anglais minuscules.
Chaque caractère du clavier est représenté par un nombre en base deux de 7 bits qui ne figurent pas dans la liste. La lettre majuscule de « N », par exemple, est représentée par les sept bits 1001110 en base 2. Pour convertir 1001110 2 en base 16, faites-le précéder de 0 et regroupez le résultat en sous-groupes de quatre bits comme suit :
| 0100 | 1110 | 2 = | 4 | E | 16
C'est 01001110 2 = 4E 16 . Pour convertir 4E 16 en base dix, procédez comme suit :
4 fois (16) 1 + E x (16) 0 = 4 x 16 + E x 1 = 4 x 16 + 14 x 1 = 64 + 14 = 78 dix
À droite de « N » dans la liste (tableau) se trouvent le nombre hexadécimal de 4E et le nombre décimal de 78.
Autre exemple, le caractère « [ » est représenté par les sept bits 1011011 en base 2. Pour convertir 1011011 2 en base 16, faites-le précéder de 0 et regroupez le résultat en sous-groupes de quatre bits comme suit :
| 0101 | 1011 | 2 = | 5 | B | 16
C'est 01011011 2 = 5B 16 . Pour convertir 5B16 en base dix, procédez comme suit :
5 fois (16) 1 +Bx (16) 0 = 5 x 16 + B x 1 = 5 x 16 + 11 x 1 = 80 + 11 = 91 dix
À droite de « [ » dans la liste (tableau) se trouvent le nombre hexadécimal de 5B et le nombre décimal de 91.
Comme autre exemple encore, le caractère du nombre décimal « 5 » est représenté par les sept bits 0110101 en base 2, et pas 0000101 en base 2. Pour convertir 0110101 2 en base 16, faites-le précéder de 0 et regroupez le résultat en sous-groupes de quatre bits comme suit :
| 0011 | 0101 | 2 = | 5 | B | 16
C'est 00110101 2 = 35 16 . Pour convertir 3516 en base dix, procédez comme suit :
3 fois (16) 1 + 5x (16) 0 = 3 x 16 + 5 x 1 = 3 x 16 + 5 x 1 = 48 + 5 = 53 dix
À droite du « 5 » dans la liste (tableau) se trouvent le nombre hexadécimal de 35 et le nombre décimal de 53.
Puisque l'ordinateur fonctionne en octets, lorsqu'une touche du clavier idéal est enfoncée, huit bits sont envoyés au microprocesseur (carte mère). Le clavier idéal est un périphérique séparé de l’unité système (de base) de l’ordinateur. Il possède un circuit électronique (IC) qui crée les sept bits et les précède d'un zéro avant de les envoyer via son câble à la carte mère de l'unité centrale. Depuis le port d'entrée (circuit d'entrée) de la carte mère, il se dirige vers le microprocesseur qui se trouve également sur la carte mère. Du microprocesseur, il va à la mémoire qui est également installée sur la carte mère.
Ainsi, lorsque la touche « N » du clavier idéal est enfoncée, huit bits 01001110 sont transmis au microprocesseur. Depuis le microprocesseur, ils sont transférés vers la mémoire où ils restent dans un emplacement mémoire sous forme d'octet. Le programmeur informatique doit garder à l’esprit que les huit bits de 01001110 2 est le même que 4E 16 ce qui équivaut à 78 dix .
Lorsque la touche « [ » du clavier idéal est enfoncée, huit bits 01011011 sont transmis au microprocesseur. Depuis le microprocesseur, ils sont transférés vers la mémoire où ils restent dans un emplacement mémoire sous forme d'octet. Le programmeur informatique doit garder à l’esprit que les huit bits de 01011011 2 est le même que 5B 16 ce qui équivaut à 91 dix .
Lorsque la touche « 5 » du clavier idéal est enfoncée, sous forme de caractère et non de nombre décimal, huit bits 00110101 sont transmis au microprocesseur. Depuis le microprocesseur, ils sont transférés vers la mémoire où ils restent dans un emplacement mémoire sous forme d'octet. Le programmeur informatique doit garder à l'esprit que les huit bits de 00110101 2 est la même chose que 35 16 ce qui est le même que 5310 dix .
Il arrive parfois qu'un programme soit en cours d'exécution et attende que le nombre décimal 5 soit saisi dans l'ordinateur. Dans cette situation, si la touche « 5 » du clavier idéal est enfoncée, le code à huit bits 00110101 est toujours transmis au microprocesseur. Puisque ce qu'il faut, c'est le nombre décimal 5, et non le caractère « 5 », un morceau de code (programme court) de la mémoire utilise le microprocesseur pour convertir le code de caractère 00110101 en base deux en nombre complémentaire à deux 00000101. 2 avant de l’envoyer vers un emplacement mémoire sous forme d’octet de complément à deux. Le programmeur informatique doit garder à l’esprit que 00000101 signifie 5 dix en base 2, et il est différent des numéros de code de 00110101 2 , 35 16 , et 53 dix ce qui signifie le caractère « 5 ». Afin d'afficher le nombre complémentaire à deux de 00000101 dans la mémoire, un autre programme court doit convertir 00000101 de la mémoire en 00110101. Il s'agit de 00110101, ce qui équivaut à 35. 16 ce qui équivaut à 53 dix qui est affiché sur le moniteur (ou imprimé sur un papier par l'imprimante).
3.9 Format des nombres à virgule flottante
Un nombre sans partie décimale est un entier. Le nombre 36 est un nombre entier. 36,375 n'est pas un entier. C'est un nombre décimal avec une partie décimale. La partie décimale de 0,375 est une fraction inférieure à 1.
36,375 est interprété sous forme décimale comme :
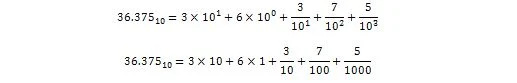
Maintenant:
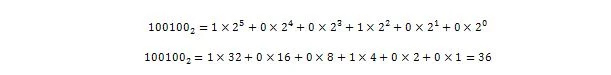
Donc 100100 2 = 3610 qui est la partie entière de 36,375 dix .
Maintenant:
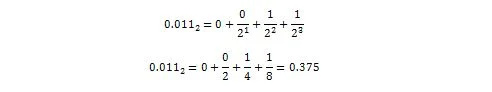
Donc 0,011 2 = 0,375 dix qui est la partie décimale de 36,375 dix .
∴ 36 375 dix = 100100,011 2
Autrement dit :
100100.011 2 = 36 375 dix
Les nombres sont représentés dans l'ordinateur en base 2 et non en base 10, toutes choses étant égales par ailleurs. Puisqu'une cellule dans un registre du microprocesseur ou une cellule en mémoire ne peut prendre que 1 ou 0, il n'y a pas de place pour stocker un point décimal. Cela pose un problème. Comme résolution, il existe la représentation à virgule flottante 32 bits simple précision IEEE-754 et la représentation à virgule flottante double précision IEEE-754 64 bits.
Format de nombre à virgule flottante 32 bits
Le nombre 100100.0112 peut s’exprimer comme suit :
100100.011 2 = 1,00100011 2 x2 +5
Le côté droit du symbole = est appelé en mathématiques la forme standard en base deux du côté gauche de 100100.011. 2 .
Maintenant, 00100011 sur 1.00100011 2 à droite du symbole =, sans le « 1 » précédent. et sans le 2 pour la base, est appelé la mantisse explicite. Dans ce cas, le point binaire est placé cinq places vers la gauche afin d'avoir le « 1 ». Ne confondez pas le point décimal et le point binaire. Le point binaire est pour la base 2, tandis que le point décimal est pour la base 10. Le « 1 ». suivi de 00100011 à droite du symbole =, sans le 2 pour la base, forme la vraie signification. Cependant, 1,00100011 est appelé la mantisse implicite.
Après le signifiant à droite se trouve le « x 2 » +5 ' expression. Avec cette expression, le +5 est appelé l'exposant. Le signe plus signifie que le point binaire doit être avancé de cinq places pour retrouver sa position d'origine normale et 2 est la base de la numérotation. L’équation précédente peut s’écrire à l’envers sous la forme :
1.00100011 2 x2 +5 = 100100,011 2
Avec la représentation à virgule flottante 32 bits, il s'agit de « 1.00100011 2 x2 +5 » qui est utilisé et pas seulement « 100100.011 2 ». Le 2 pour la base n'est pas enregistré. La représentation à virgule flottante 32 bits pour le « 1.00100011 2 x2 +5 ' nombre, qui est égal à 36,375 dix = 100100,011 2 , est présenté dans le tableau suivant :

Il y a des positions de 32 bits numérotées à partir de l'extrémité droite, en commençant par 0. Le premier bit à l'extrémité gauche est le bit de signe. Si le nombre est positif, ce bit est 0. Si le nombre est négatif, ce bit est 1 (-1 est composé de deux caractères et ne peut être placé dans aucune cellule). Le 1.00100011 2 x2 +5 ce qui est égal à 36,375 dix qui est également égal à 100100,011 2 est un nombre positif. Le premier bit est donc 0.
Il y a huit positions de bits pour l'exposant, allant de la position 30 à la position 23 inclusivement. Or, l’exposant qui y est écrit est 10000100 2 ce qui est égal à 132 dix . L’exposant du nombre d’intérêt est en réalité +5 de la base de deux. Alors, que se passe-t-il ?
Désormais, au format 32 bits, un exposant de 0 s'écrit 01111111. 2 ce qui est égal à 127 dix . Le +5 dix est +101 2 . Donc, en arrivant à 10000100 2 dans la partie exposant du tableau, 101 2 a été ajouté à 01111111 2 , en conséquence. Cela signifie que 5 a été ajouté à 127 pour avoir 132 dix .
Le signifiant, sans « 1 », a pris les positions 22 jusqu'à 15 inclusivement. Notez que le 1 de « 1 ». n'a pas été indiqué dans la chaîne de 32 bits. Ce n’est jamais indiqué – acceptez-le. Le reste des cellules jusqu'à la position 0 sont remplis de zéros.
Si l'exposant réel est -5, alors 5 est soustrait de 127 dix avoir 122 dix . Cela correspond à soustraire 101 2 du 01111111 2 avoir 01111010 2 .
Avec toute l'illustration précédente, le nombre +1 qui est égal à 1,0 x 2 0 = 1,0 x 1 = 1,0 est représenté par :

Notez que le « 1 ». de 1,0 x 2 0 n’est pas indiqué dans le format. Ce n’est jamais indiqué. La prochaine fraction mixte qui devient positive après 1,0 est :

Notez le 1 à l’extrémité droite. Cette représentation est le nombre :

La différence entre 1,0000001192092896 et 1,0 est :
1,0000001192092896 – 1,0 = 0,0000001192092896
Les nombres avec parties décimales sont des fractions mixtes. Toutes les fractions comprises entre 1 et 1 ne sont pas toutes dix et 2 dix peut être représenté dans l’ordinateur. On peut supposer que le plus petit écart fractionnaire entre les nombres mixtes consécutifs au format à virgule flottante 32 bits est de 0,0000001192092896. Attendez-vous à ce que l'intervalle de double précision soit plus petit. Reportez-vous à l'illustration suivante.
Représentant le nombre, 0,0 ne suit pas les arguments précédents. La représentation de 0,0 est déclarée et doit être apprise comme telle. Pour représenter 0,0, toutes les cellules de la mantisse sont 0 et toutes les cellules de l'exposant sont également nulles. Le bit de signe peut être 0 ou 1. Malheureusement, cela donne lieu à un 0 positif et à un 0 négatif comme suit :

Dans la vraie vie, il n’y a qu’un zéro. Le positif 0 et le négatif 0 n’existent pas. Cependant, 0 est généralement considéré comme positif. Le positif 0 et le négatif 0 existent ici en raison de cette description de format particulière. La droite numérique (voir ci-dessus) peut également avoir +0 et -0, mais un seul zéro existe.
Format de nombre à virgule flottante 64 bits
Le format à virgule flottante 64 bits est similaire au format 32 bits, mais avec les différences suivantes :
- Il y a 64 bits pour représenter un nombre.
- Après le bit de signe, il y a 11 bits pour le nombre d'exposant.
- Le nombre d'exposant pour l'indice zéro (2 0 ) vaut 1023 dix = 01111111111 2 .
- Les onze bits sont suivis de 52 bits pour la mantisse explicite.
- Il propose une plage de nombres plus large que le format 32 bits.
Notez que le « 1 ». qui est au début de la mantisse n'est toujours pas inclus parmi les 64 bits, tout comme il n'est pas inclus parmi les 32 bits pour le format 32 bits.
L'une des différences les plus importantes entre le format 64 bits et le format 32 bits est que la différence entre les fractions mixtes consécutives au format 64 bits est inférieure à celle du format 32 bits.
Au format 64 bits, l'intervalle (écart) entre 1,0 et la fraction mixte suivante peut être calculé comme suit :
1.0 est
0 01111111111 000000000000000000000 00000000000 0000000000000000000000 2
Cela équivaut au « 1 », qui n'a pas été indiqué dans la chaîne, multiplié par 2 élevé à la puissance (indice) 0 (l'exposant étant 1023). dix = 01111111111 2 pour 2 0 = 1). La chaîne est 1,0 x 2 0 .
La prochaine fraction mixte supérieure à 1,0 est :
0 01111111111 000000000000000000000 00000000000 0000000000000000000001 2
Cela équivaut à « 1 ». qui n'est pas indiqué dans la chaîne, suivi de 51 zéros, puis de 1, multiplié par 2 élevé à la puissance 0 (l'exposant étant 1023 dix = 011111111112 2 pour 2 0 = 1). C'est la même chose que :
+2 0 × (1 + 2− -52 ) ≈ 1,0000000000000002
Le ≈ signifie approximativement égal à.
Maintenant:
1,0000000000000002 – 1,0 ≈ 0,0000000000000002
La valeur d'intervalle correspondante pour un format 32 bits est 0,0000001192092896 ≈ 0,00000012.
0,0000000000000002 est beaucoup plus petit que 0,00000012. Ainsi, il y a beaucoup plus de fractions mixtes entre deux entiers consécutifs (par exemple 3 et 4) au format 64 bits qu'il n'y en a entre deux entiers consécutifs au format 32 bits.
Le nombre de fractions mixtes entre deux entiers consécutifs sur la droite numérique est infini. Ainsi, aucun format (par exemple 32 bits ou 64 bits) ne peut fournir toutes les fractions mixtes entre deux entiers consécutifs (nombres entiers). Plus l'écart (intervalle) entre deux entiers consécutifs fourni par un format (par exemple 32 bits ou 64 bits) est petit, plus le nombre de fractions mixtes entre les entiers consécutifs est grand (pour la droite numérique).
Les raisons pour lesquelles le format 64 bits est décrit comme ayant une précision double ou supérieure par rapport au format 32 bits sont que l'intervalle entre deux fractions mixtes consécutives délimitées par deux entiers consécutifs pour le format 64 bits est plus petit que les 32 bits correspondants. -intervalle de format de bits. De plus, il y a plus de fractions mixtes possibles entre deux entiers bornés pour le format 64 bits que pour le format 32 bits.
Conversion d'une partie décimale (fraction) d'un nombre décimal en partie binaire
Le 36,375 est un nombre décimal avec la partie décimale de « .375 ». La partie décimale de « .375 » est une fraction comprise entre zéro et un. Le 0,5 en base dix a la même valeur que 1/2 en base deux. Le 0,5 dix qui s'exprime avec le développement en base deux est :
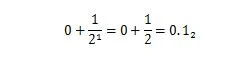
Ce n'est pas 0,101 2 ce qui signifie 0,625 dix . La partie décimale d'un nombre décimal a sa partie binaire équivalente pour le nombre binaire correspondant. Donc, pour convertir un nombre décimal comme 36,375 dix en base deux, convertissez 36 en binaire, puis convertissez .375 également en binaire. Ensuite, joignez les deux résultats avec le point binaire. Les méthodes pour convertir les deux sections sont différentes. Comment convertir un entier décimal en base 2 est expliqué au chapitre 1.
Pour convertir la fraction décimale en fraction binaire, suivez les étapes suivantes :
- Multipliez la fraction décimale (partie décimale) par 2. L'entier qui en résulte est le premier chiffre binaire.
- Répétez l’étape précédente avec le résultat décimal fractionnaire pour obtenir le chiffre binaire suivant.
- Continuez à répéter l’étape précédente jusqu’à ce que le résultat fractionnaire décimal soit 0,0000—.
Exemple : Convertir la partie fractionnaire de 36,375 dix à la partie fractionnaire équivalente en base deux.
Solution:
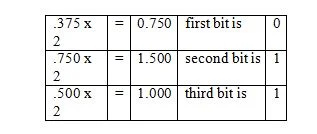
Notez qu'à la troisième étape, .500 a été multiplié par 2 et non par 1.500. La fraction binaire correspondante est lue dans la dernière colonne en partant du haut. Et donc le résultat suivant est :
.375 dix = 0,011 2
Conversion d'une partie binaire (fraction) d'un nombre binaire en partie décimale
Pour y parvenir, développez la fraction binaire en puissances réciproques de 2.
Exemple : Convertir la partie fractionnaire de 100100,011 2 à la partie fractionnaire équivalente en base dix.
Solution:
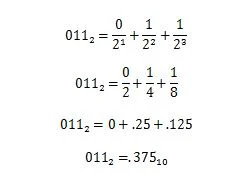
3.10 Préfixes numériques en informatique
Dans la vie normale, 1 kilo signifie 1000 qui s'abrège en k (minuscule) comme en 1kg. En informatique, 1 kilo signifie 2 dix = 1024, mais est abrégé en K (majuscule) comme en 1Kbits. Dans la vie normale, 1 méga signifie 1 000 000, ce qui est abrégé en M (majuscule) comme en 1Mg. En informatique, 1 méga signifie 2 vingt = 1 048 576 = 2 dix x2 dix = 1024 x 1024 = 1 048 576 et est toujours abrégé en M (majuscule) comme en 1Mbits. Dans la vie normale, 1 giga signifie 1 000 000 000 est abrégé en G (majuscule) comme en 1Gg. En informatique, 1 giga signifie 2 30 = 1 073 741 824 = 2 dix x2 dix x2 dix = 1024 x 1024 x 1024 = 1 073 741 824 et est toujours abrégé en G (majuscule) comme en 1Gbits. Le tableau suivant donne la signification de quatre préfixes dans la vie normale et en informatique :
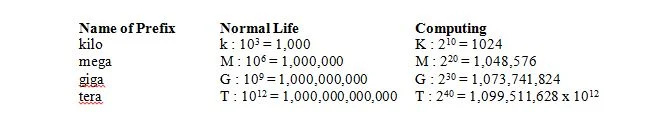
3.11 Problèmes
Il est conseillé au lecteur de résoudre tous les problèmes d'un chapitre avant de passer au chapitre suivant.
- Tracez une droite numérique avec des nombres entiers de -10 à +10.
- Additionnez les nombres binaires suivants en complément à deux de 8 bits : 101010 2 et 1111 2 .
- Utilisez uniquement l'approche du complément à deux sur 8 bits pour soustraire le nombre binaire de 1111 2 à partir du nombre binaire 101010 2 .
- Trouver le produit de 10110 2 x1101 2 en base deux.
- Divisez 36 375 dix par 1000 dix en décimal et en binaire, et comparez les résultats.
- Utilisez les 8 bits de votre choix pour illustrer les logiques AND, OR, XOR, Invert, Shift Right, Shift Left, Rotate Right et Rotate Left. Chaque octet doit contenir un mélange de 1 et de 0.
- a) Écrivez le code numérique du caractère ASCII de zéro en hexadécimal, binaire et décimal.
b) Écrivez le code numérique du caractère ASCII « 1 » en hexadécimal, binaire et décimal.
c) Écrivez le code numérique du caractère ASCII de « A » en hexadécimal, binaire et décimal.
d) Écrivez le code numérique du caractère ASCII de « a » en hexadécimal, binaire et décimal. - Convertir 49,49 dix en base deux. Convertissez votre résultat au format à virgule flottante IEEE 32 bits.
- a) En quoi le format à virgule flottante IEEE 64 bits est-il différent du format 32 bits ?
b) Donnez les deux raisons liées pour lesquelles le format 64 bits est décrit comme ayant une précision double ou supérieure sur le
Format 32 bits.