Cet article va nous apprendre le fonctionnement de FFT dans MATLAB.
Comprendre la FFT
Le Transformée de Fourier rapide (FFT) représente une technique spéciale qui nous aide à comprendre les signaux différemment. Normalement, les signaux sont affichés sous forme de séquences de nombres qui changent dans le temps, mais avec FFT, nous pouvons voir quelles sont les différentes fréquences présentes dans le signal et leur intensité. C'est comme décomposer un signal en ses notes de musique et voir à quel point chaque note est forte.
Le FFT L'algorithme effectue beaucoup de calculs complexes sur les données du signal. Il prend le signal et le divise en parties plus petites, puis calcule les fréquences et leurs forces pour chaque partie. Enfin, il combine tous les résultats pour nous donner une image du contenu fréquentiel du signal, des relations de phase et d'autres caractéristiques importantes.
Cette technique est utilisée dans de nombreux domaines car elle nous aide à mieux analyser et comprendre les signaux. Par exemple, dans traitement de signal , on peut utiliser FFT pour filtrer les bruits indésirables ou détecter des motifs spécifiques. Dans analyse audio , nous pouvons identifier différents sons ou analyser la qualité d'un enregistrement audio. Dans traitement d'image , FFT peut nous aider à analyser les fréquences spatiales dans l'image. Et dans les télécommunications, FFT est utilisé pour transmettre et recevoir efficacement des signaux.
Comment utiliser FFT dans MATLAB
MATLAB fournit une fonction intégrée appelée fft qui nous permet d'effectuer Transformée de Fourier rapide (FFT) calculs sur les signaux. Cette fonction est simple d'utilisation et offre différentes possibilités d'analyse et de manipulation des signaux dans le domaine fréquentiel :
La syntaxe d'utilisation du FFT fonctions dans MATLAB est donnée ci-dessous:
F = fft ( X )F = fft ( x,n )
F = fft ( x,n,dim )
Ici:
F= fft(x) donne le calcul de la Transformée de Fourier discrète (DFT) de x en utilisant le Transformée de Fourier rapide (FFT) algorithme.
- Si x représente un vecteur, fft(x) donne la transformée de Fourier du vecteur.
- Si x représente une matrice, fft(x) fournit la transformée de Fourier de chaque colonne en traitant chaque colonne comme un vecteur.
F = fft(x,n) donne une DFT à n points. F a la même taille que x lorsqu'aucune valeur n'est fournie.
- Si x est un vecteur et que sa longueur est inférieure à n, x obtient un remplissage avec des zéros de fin jusqu'à ce qu'il atteigne n.
- Si x est un vecteur et que sa longueur dépasse n, il est tronqué à cette longueur n.
- Si x est une matrice, chaque colonne est considérée comme un cas vectoriel.
F = fft(x,n,dim) donne la transformée de Fourier le long de la dimension donnée dim. Disons, fft(x, n, 2) donne la transformée de Fourier à n points pour chaque ligne si x représente une matrice.
Les exemples suivants illustrent le fonctionnement de FFT fonction dans MATLAB.
Exemple 1
On peut utiliser FFT dans MATLAB pour démontrer la génération et l'analyse d'un signal avec des composantes de fréquence spécifiques et un bruit aléatoire.
Par exemple:
ls = 2000 ;fs = 1500 ;
ts = 1 /fs;
télé = ( 0 :ls- 1 ) *ts ;
f = 0,6 * sans ( 2 * pi * cinquante *la télé ) + 3 * Randn ( taille ( la télé ) ) + sans ( 2 * pi * 120 *la télé ) ;
parcelle ( 1000 *la télé ( 1 : cinquante ) ,F ( 1 : cinquante ) )
xétiquette ( 'télé (ms)' )
yétiquette ( 'f(télé)' )
titre ( 'Signal corrompu ayant un bruit aléatoire à moyenne nulle' )
F = fft ( F ) ;
PS2 = abdos ( F/ ls ) ;
PS1 = PS2 ( 1 : ls / 2 + 1 ) ;
PS1 ( 2 :fin- 1 ) = 2 *PS1 ( 2 :fin- 1 ) ;
f = fs* ( 0 : ( ls / 2 ) ) / ls ;
parcelle ( f, PS1 )
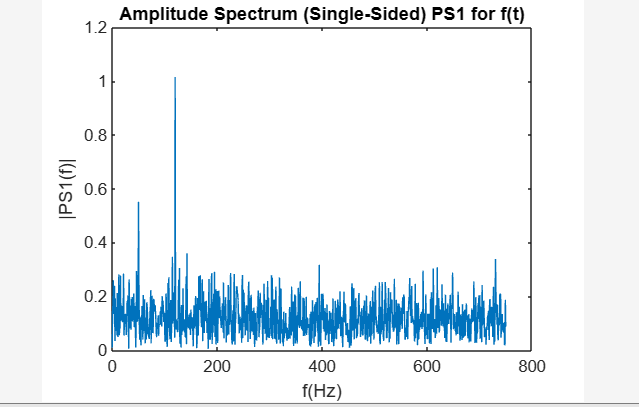
titre ( 'Spectre d'amplitude (unilatéral) PS1 pour f(t)' )
xétiquette ( 'f(Hz)' )
ylabel ( '|PS1(f)|' )
Le code fourni génère un signal d'une longueur de 2000 échantillons (ls) , une fréquence d'échantillonnage de 1 500 Hz (fs) , et un période d'échantillonnage (ts) . Le vecteur temps (tv) est créé en fonction de ces paramètres. Le signal F est composé d'une combinaison de composantes sinusoïdales à 50 Hz et 120 Hz, ainsi que d'un bruit aléatoire de moyenne nulle. Il est ensuite tracé avec un segment des 50 premiers échantillons. Le code calcule en outre le FFT du signal et calcule la spectre d'amplitude (PS1) . Enfin, le spectre d'amplitude est tracé par rapport aux fréquences correspondantes (f) en Hz.
Exemple 2
Voici un autre exemple qui utilise le FFT fonction dans MATLAB pour la transformation de l'impulsion gaussienne dans le domaine temporel vers le domaine fréquentiel.
fs = 500 ;ts = - 0,5 : 1 /fs : 0,5 ;
ls = longueur ( ts ) ;
f = 1 / ( 4 * sqrt ( 2 * pi * 0,02 ) ) * ( exp ( -ts.^ 2 / ( 2 * 0,02 ) ) ) ;
parcelle ( ts, f )
xétiquette ( 'Temps (t)' )
yétiquette ( 'f(t)' )
titre ( 'Dans le domaine temporel' )
ex = 2 ^ nextpow2 ( ls ) ;
f = fs* ( 0 : ( par exemple/ 2 ) ) /par exemple;
F = fft ( f,np ) ;
PF = abdos ( F/np ) ;
parcelle ( f,PF ( 1 :par exemple/ 2 + 1 ) )
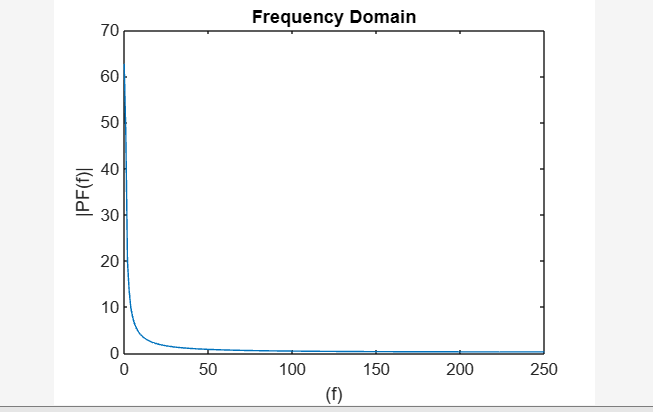
xétiquette ( '(F)' )
yétiquette ( '|PF(f)|' )
titre ( 'Domaine de fréquence' )
Le code fourni génère un signal d'impulsion gaussien dans le domaine temporel et analyse son contenu fréquentiel en utilisant le Transformée de Fourier rapide (FFT) dans MATLAB. Le signal dans le domaine temporel est tracé, puis le FFT est effectuée pour obtenir la représentation dans le domaine fréquentiel. La résultante spectre d'amplitude est tracé en fonction des fréquences correspondantes.
Exemple 3
L'exemple suivant génère trois signaux sinusoïdaux avec des fréquences différentes et les trace dans le domaine temporel à l'aide de la FFT fonction dans MATLAB.
fs = 2500 ;ts = 1 /fs;
ls = 3000 ;
t = ( 0 :ls- 1 ) *ts ;
r1 = sans ( 3 * pi * 60 *t ) ;
r2 = sans ( 3 * pi * 140 *t ) ;
r3 = sans ( 3 * pi * 350 *t ) ;
f = [ r1 ; r2; r3 ] ;
pour k = 1 : 3
sous-parcelle ( 3 , 1 ,k )
parcelle ( t ( 1 : 250 ) ,F ( k, 1 : 250 ) )
titre ( [ 'Ligne Non ' , num2str ( k ) , ' (Dans le domaine temporel)' ] )
fin
par exemple = 2 ^ nextpow2 ( ls ) ;
ré = 2 ;
F = fft ( f,np,d ) ;
PS2 = abdos ( F/ ls ) ;
PS1 = PS2 ( :, 1 :par exemple/ 2 + 1 ) ;
PS1 ( :, 2 :fin- 1 ) = 2 *PS1 ( :, 2 :fin- 1 ) ;
pour k= 1 : 3
sous-parcelle ( 3 , 1 ,k )
parcelle ( 0 : ( fs/np ) : ( fs/ 2 -fs/np ) ,PS1 ( k, 1 :par exemple/ 2 ) )
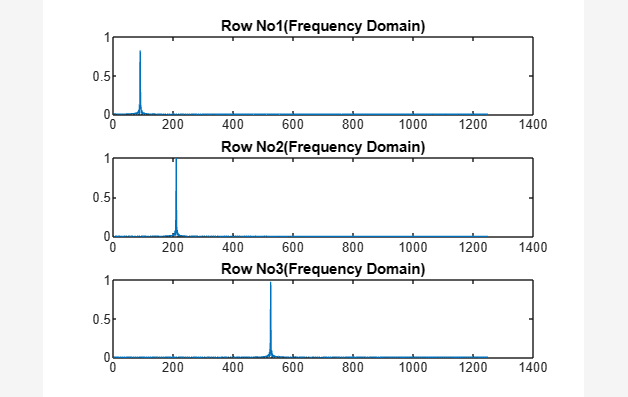
titre ( [ 'Ligne Non' , num2str ( k ) , '(Domaine de fréquence)' ] )
fin
Dans le code ci-dessus, trois ondes sinusoïdales, r1, r2 et r3 sont affichées dans la fenêtre de sortie dans le domaine temporel. Le signal de domaine fréquentiel 'PS1' est créé en utilisant la fonction FFT sur les ondes pour calculer chacun de leurs spectres d'amplitude unilatéral individuels.
Conclusion
Le FFT est un outil précieux qui nous aide à appréhender différemment les signaux en analysant leur contenu fréquentiel. Avec la fonction intégrée de MATLAB, fft, performant FFT les calculs sur les signaux deviennent commodes. Cette fonction nous permet d'apprendre des détails cruciaux sur les différentes fréquences et les intensités relatives de ces fréquences en convertissant les données du domaine temporel au domaine fréquentiel. Le guide ci-dessus est crucial pour mieux comprendre les caractéristiques du signal et prendre des décisions éclairées dans différentes applications.