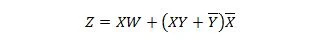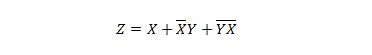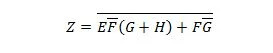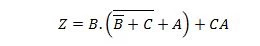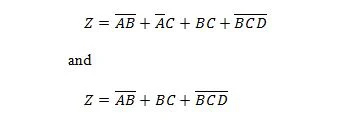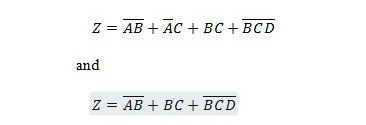Chapitre 2 : Algèbre booléenne et ses composants informatiques associés

Chapitre 2 : Algèbre booléenne et ses composants informatiques associés

2.1 Opérateurs booléens de base

Supposons que moi (l’auteur) suis grand et que vous (le lecteur) êtes grand. Si quelqu’un vous demande si nous sommes tous les deux grands, vous répondrez « Oui » (vrai). S'il vous demande si nous sommes tous les deux petits, vous répondriez « Non » (faux). Si vous êtes petit et que je suis grand, et qu'il vous demande si vous ou moi sommes grands, votre réponse serait « Oui » (vrai). S’il vous demande si vous et moi sommes grands, vous n’aurez pas de réponse. Vous pourriez poursuivre en disant que la dernière question ne devrait pas être posée ou qu’elle n’a pas de réponse. Eh bien, je veux que vous (le lecteur) sachiez qu’aujourd’hui, dans certaines circonstances, la question devrait être posée.

En biologie, une personne est soit grande, soit petite. Ce sont les conditions « environnementales » qui font que la personne est de taille moyenne. Un scientifique, George Boole, a défini un ensemble de réponses ou de règles pour ce type de questions. Nous apprendrons ces règles dans cette section du cours de carrière en ligne (chapitre). Ces règles sont aujourd’hui utilisées en informatique, en programmation, en électronique et en télécommunications. En fait, sans ces règles, vous n’auriez pas d’ordinateur, comme c’est courant aujourd’hui ; vous n'auriez pas non plus de programmation, comme c'est courant aujourd'hui.

Vrai ou faux
Une simple déclaration en langage humain est soit vraie, soit fausse en soi. Si je dis : « Je suis grand », c’est soit vrai, soit faux. Si je dis « tu es grand », c’est soit vrai, soit faux. Si je suis grand et que vous êtes petit, et que la question est posée si vous et moi sommes grands, en logique booléenne, une réponse vraie ou fausse doit être donnée. Lequel de ces deux faut-il donner ? Boole n'a pas vraiment répondu à cette question. Il nous a simplement proposé un ensemble de règles à suivre. La bonne nouvelle est que lorsque vous suivez ces règles dans leur bon contexte, vous n’avez aucune ambiguïté. Grâce à ces règles, nous disposons aujourd’hui d’ordinateurs et de programmation. Les règles vous sont données maintenant. Les règles ne peuvent pas vraiment être expliquées ; vous les acceptez simplement. Les règles sont réparties sous trois titres : ET, OU et NON.

ET
La question peut être posée si vous ET moi sommes grands. Ma taille et votre taille sont ensuite combinées par l'ensemble de règles AND. Voici les règles ET à suivre :

faux ET faux = faux
faux ET vrai = faux
vrai ET faux = faux
vrai ET vrai = vrai

Maintenant, que grand soit vrai et court soit faux. Cela signifie que si je suis petit ET que vous êtes petit, vous et moi sommes petits. Si je suis petit ET que tu es grand, toi et moi sommes petits ; c'est la réponse booléenne que vous devez accepter. Si je suis grand ET que vous êtes petit, vous et moi sommes petits. Si je suis grand ET que tu es grand, toi et moi sommes grands. Ce sont toutes des règles ET booléennes que vous (le lecteur) devez simplement accepter.

OU
La question peut être posée si vous OU moi êtes grand. Ma taille et votre taille sont ensuite combinées par l'ensemble de règles OR. Voici les règles OU à suivre :

faux OU faux = faux
faux OU vrai = vrai
vrai OU faux = vrai
vrai OU vrai = vrai

Encore une fois, que grand soit vrai et court soit faux. Cela signifie que si je suis petit OU si vous êtes petit, vous OU moi sommes petits. Si je suis petit OU si vous êtes grand, vous ou moi sommes grands. Si je suis grand OU si vous êtes petit, vous OU moi sommes grands. Si je suis grand OU si vous êtes grand, vous ou moi sommes grands. Ce sont toutes des règles booléennes que vous devez accepter.

PAS
Or, en logique booléenne, il n’existe que deux états (réponses possibles). Autrement dit, si vous n’êtes PAS grand, vous êtes petit. Si vous n’êtes PAS petit, vous êtes grand ; rien d'autre. Voici les règles NON à suivre :

PAS faux = vrai
PAS vrai = faux

Supposons que vous disposez d’une ficelle (ou d’un ressort) que vous pouvez étendre (tirer). Tant que la corde est dans son état naturel, si je dis « PAS courte », vous l’allongeriez ; telle est l'interprétation. Pendant que la chaîne est étendue, si je dis « PAS longue », vous lui permettrez de se contracter ; telle est l'interprétation.

Vous devez mémoriser toutes les règles données dans leurs différentes catégories.

Plus de deux opérandes
Dans un langage informatique, AND, OR et NOT sont chacun appelés un opérateur. Pour l’opérateur NOT, vous n’avez besoin que d’un seul opérande (valeur pour un opérateur) pour avoir une réponse. Pour les opérateurs AND ou OR, vous pouvez avoir plus de deux opérandes. Les cas précédents montrent deux opérandes pour AND et OR. Vous pouvez avoir trois opérandes pour AND comme suit :

faux ET faux ET faux = faux
faux ET faux ET vrai = faux

Ce sont deux lignes ; chacun a deux opérateurs ET. Il y a en réalité neuf lignes lorsque les opérandes sont au nombre de trois. Avec l'opérateur AND, seule la dernière ligne (neuvième ligne) est égale à vrai ; toutes les lignes précédentes sont fausses. Notez qu'avec deux opérandes pour AND, seule la dernière ligne est toujours vraie ; les trois lignes précédentes sont fausses. Lorsque les opérandes sont au nombre de quatre, il y a 16 lignes et seule la dernière ligne est vraie pour l'opérateur AND.

Le modèle pour AND et le modèle pour OR sont différents. Avec trois opérandes pour deux opérateurs OU, il y a aussi neuf lignes et seule la première ligne, cette fois, est fausse. La deuxième à la neuvième ligne est vraie. Notez qu'avec deux opérandes pour OR, seule la première ligne est toujours vraie ; les trois lignes restantes sont fausses. Lorsque les opérandes sont au nombre de quatre pour OU, il y a également 16 lignes.

L'opérateur NOT ne traite qu'un seul opérande. Le NON faux est vrai et le NON vrai est faux.

2.2 Table de vérité à deux opérandes et leurs composants électroniques

En mathématiques, il existe un sujet appelé algèbre. Une petite partie a été vue dans le chapitre précédent. Il existe une sorte d’algèbre appelée algèbre booléenne. En algèbre booléenne, vrai est identifié par le chiffre en base deux qui est 1 et faux est identifié par le chiffre en base deux qui est 0.

Les composants internes de l'unité informatique sont des composants électroniques. L'unité centrale du système informatique comporte des composants électroniques numériques. L’opération ET est effectuée par un petit composant électronique appelé porte ET. L'opération OU est effectuée par le petit composant électronique appelé porte OU. L'opération NOT est effectuée par le petit composant électronique appelé porte NOT. Un trop grand nombre de ces portes peuvent se trouver dans une puce de circuit intégré (IC).

ET Table de Vérité et sa porte
Le tableau suivant donne la table de vérité ET et son symbole de porte ET (petit circuit) :

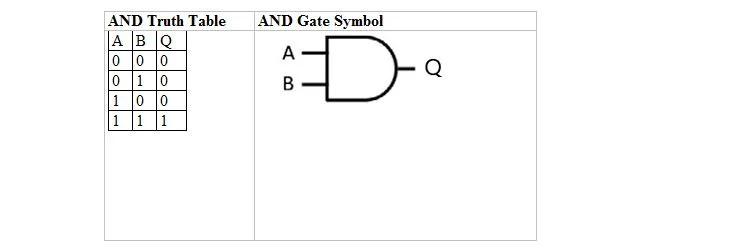
Pour la table de vérité ET et sa porte, A ainsi que B sont deux variables d'entrée. Q est la variable de sortie. A vaut 1 ou 0. B vaut 1 ou 0. Q vaut 1 ou 0. La table de vérité ET avec des 1 et des 0 est la même que la disposition de vérité ET vrai/faux précédente (table). L’équation ET est :

UN . B = Q

où le point (.) signifie AND (booléen). Le point peut être omis pour avoir AB = Q ce qui signifie la même chose (ET).

Remarque : Les bits de A et B dans les quatre lignes, par paires, sont les quatre premiers nombres en base deux commençant par 0 (ou 00), c'est-à-dire 00, 01, 10, 11.

Le tableau suivant donne la table de vérité OU et son symbole de porte OU (petit circuit) :

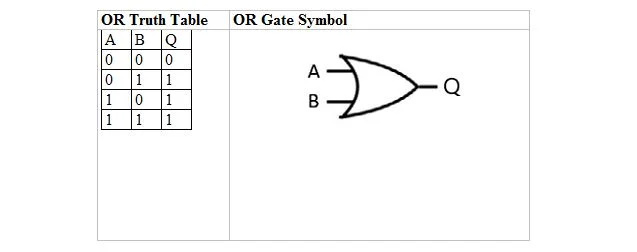
Pour la table de vérité OU et sa porte, A ainsi que B sont deux variables d'entrée. Q est la variable de sortie. La table de vérité OU avec des 1 et des 0 est la même que la précédente disposition de vérité OU vrai/faux (table).

L’équation OU est :

A + B = Q

Où le + signifie ici booléen OU et non une addition. L'équation se lit comme « A ou B égal à Q ».

Le tableau suivant donne la table de vérité NON et son symbole de porte NON (petit circuit) :

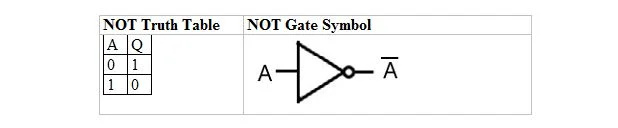
La table de vérité NOT ou porte NOT n’a qu’une seule entrée et une seule sortie. Lorsque l'entrée est 0, la sortie est 1. Lorsque l'entrée est 1, la sortie est 0. La porte NON effectue une sorte d'inversion. La variable de sortie est la même que la variable d'entrée, mais avec une barre (surlignée). La table de vérité NON avec des 1 et des 0 est la même que la précédente disposition de vérité vrai/faux OU (table).

L’équation NOT est :

A = Q

Où Q = A et la barre au-dessus de A signifie ici complément. Le complément de 0 est 1 et le complément de 1 est 0. La porte NON est également connue sous le nom de porte INVERSANTE.

Ce sont les tables de vérité fondamentales (ou racines) et leurs portes (petits circuits) en électronique numérique (avec l'algèbre booléenne). Les trois autres tables de vérité données dans l'illustration suivante et leurs portes sont fournies à titre de commodité et sont basées sur les trois tables de vérité précédentes.

Il existe une table de vérité et une porte dérivées de la table et de la porte de vérité ET. On les appelle la table de vérité NAND (pour NOT AND) et la porte NAND correspondante. La table de vérité NAND et sa porte NAND sont :

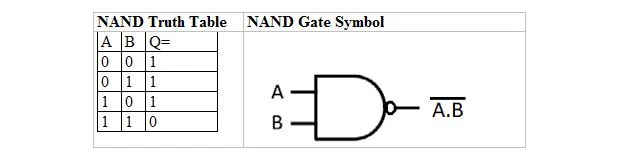
Pour obtenir la table de vérité NAND, accédez à la sortie de la table de vérité AND et remplacez chaque chiffre par son complément. Le complément de 0 est 1 et le complément de 1 est 0. La porte NAND est comme la porte ET, mais a un petit cercle avant la ligne de sortie. L'équation NAND est :

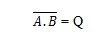
Où signifie le complément du résultat de « A » ET « B ». La barre (au-dessus de la ligne) est représentée dans le portail par le petit cercle. Notez que le point entre A et B peut être omis.

Il existe une autre table de vérité et une autre porte dérivées de la table et de la porte de vérité OU. On les appelle la table de vérité NOR (pour NOT OR) et la porte NOR correspondante. La table de vérité NOR et sa porte NOR sont :

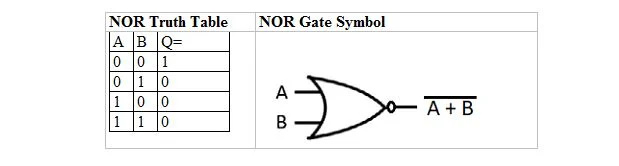
Pour obtenir la table de vérité NOR, accédez à la sortie de la table de vérité OU et remplacez chaque chiffre par son complément. Le complément de 0 est 1 et le complément de 1 est 0. La porte NI est comme la porte OU, mais a un petit cercle avant la ligne de sortie. L'équation NOR est :

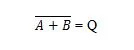
Où 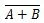désigne le complément du résultat de « A » OU « B ». La barre (surligne) est représentée dans le portail par le petit cercle.

OU exclusif (XOR)
La table de vérité de la porte OU est la suivante :

En anglais normal, il n'est pas clair si la dernière ligne de 1 OU 1 doit donner 1 ou 0. Ainsi, en algèbre booléenne, il existe deux types de tables de vérité OU et deux portes correspondantes. Avec le OU normal, la dernière ligne de 1 OU 1 donne 1. L'autre type de OU est le OU exclusif (XOR) où les trois premières lignes sont les mêmes que les trois premières lignes du OU normal (y compris la sortie). Cependant, pour la quatrième et dernière ligne, 1 OU 1 donne 0.

Le tableau suivant donne la table de vérité XOR et son symbole de porte XOR (petit circuit) :

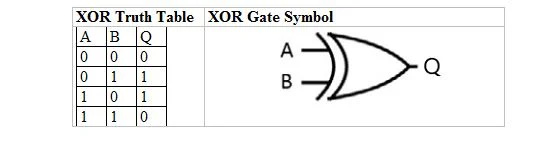
Pour la table de vérité XOR et sa porte, « A » ainsi que « B » sont deux variables d'entrée. « Q » est la variable de sortie.

L'équation XOR est :

UNE ⊕ B = Q

Où le ⊕ signifie ici XOR booléen.

Le OU normal signifie l’un ou les deux. OU exclusif signifie strictement soit et pas les deux.

2.3 Postulats booléens

Les postulats sont des hypothèses sur la base desquelles certaines conclusions sont tirées. Il existe dix postulats booléens issus des équations AND, OR et NOT (tables de vérité). Ces équations sont également appelées fonctions. Les fonctions fondamentales sont recopiées comme suit :

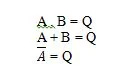
Ce sont les fonctions fondamentales (équations) de l’algèbre booléenne. Les trois autres équations (fonctions) suivantes ne sont pas des fonctions fondamentales :

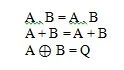
Bien que cette dernière fonction soit particulière, elle n’est pas considérée comme une fonction fondamentale.

Les postulats booléens sont les suivants :

De la fonction ET
dix . 0 = 0
vingt . 1 = 0
3)1. 0 = 0
4)1. 1 = 1

De la fonction OU
5) 0 + 0 = 0
6) 0 + 1 = 1
7) 1 + 0 = 1
8) 1 + 1 = 1

De la fonction NOT
9) 0 = 1
10) 1 = 0

Note: Ces postulats ne sont que les lignes des tables de vérité ET, OU et NON qui sont exprimées de manière indépendante. Le lecteur doit mémoriser les postulats donnés.

2.4 Propriétés booléennes

Une propriété est comme une caractéristique de quelque chose. Les propriétés booléennes sont des équations dérivées des postulats booléens. Dans cette section, les propriétés sont simplement données sans leurs dérivations puis utilisées par la suite. Il existe vingt-cinq propriétés regroupées sous dix rubriques comme suit :

Propriétés de la fonction ET

Propriété 1 :

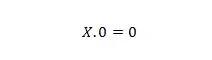
Où X peut être 1 ou 0. Cela signifie que peu importe ce que X est, le résultat est toujours 0.

Remarque : Une variable ne doit pas nécessairement être A ou B ou C ou D. Une variable peut être W ou X ou Y ou Z ou toute autre lettre.

Propriété 2 :

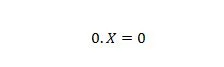
Où X peut être 1 ou 0. Notez que la différence entre la propriété 1 et la propriété 2 est que sur le côté gauche du signe égal des deux équations, les positions de X et 0 sont inversées.

Propriété 3 :

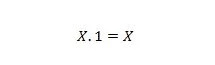
Si X vaut 0, alors 0, 1 = 0. Si X vaut 1, alors 1, 1 = 1.

Propriété 4 :

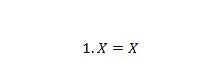
Si X est 0, alors 1. 0 = 0. Si X est 1, alors 1. 1 = 1. Notez que la différence entre la propriété 3 et la propriété 4 est que sur le côté gauche des deux équations, les positions de X et 1 sont intervertis.

Propriétés de la fonction OU

Propriété 5 :

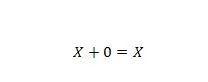
Où X peut être 1 ou 0. Cela signifie que si X est 0, le résultat est 0. Si X est 1, le résultat est 1.

Propriété 6 :

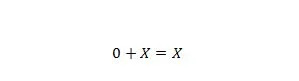
Où X peut être 1 ou 0. Notez que la différence entre la propriété 5 et la propriété 6 est que sur le côté gauche des deux équations, les positions de X et 0 sont inversées.

Propriété 7 :

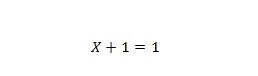
Si X vaut 0, alors 0 + 1 = 1. Si X vaut 1, alors 1 + 1 = 1.

Propriété 8 :

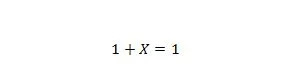
Si X vaut 0, alors 1 + 0 = 1. Si X vaut 1, alors 1 + 1 = 1. Notez que la différence entre la propriété 7 et la propriété 8 est que sur le côté gauche des deux équations, les positions de X et 1 sont intervertis.

Propriétés concernant la combinaison d'une variable avec elle-même ou son complément

Propriété 9 :

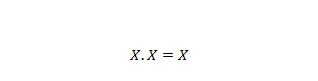
Autrement dit : si X est 0, alors 0 . 0 = 0. Si X vaut 1, alors 1 . 1 = 1.

Propriété 10 :

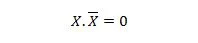
Autrement dit : si X vaut 0, alors 0, 1 = 0. Si X vaut 1, alors 1, 0 = 0.

Pour les variables consécutives, cette propriété devient :

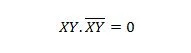
Propriété 11 :

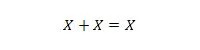
Autrement dit : si X vaut 0, alors 0 + 0 = 0. Si X vaut 1, alors 1 + 1 = 1 (à partir du OU normal).

Propriété 12 :

Autrement dit : si X vaut 0, alors 0 + 1 = 1. Si X = 1, alors 1 + 0 = 1.

Autrement dit : si X vaut 0, alors 0 + 1 = 1. Si X = 1, alors 1 + 0 = 1.

Double complémentation

Propriété 13 :

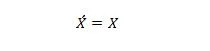
Lorsque X du côté gauche est 0, X du côté droit devient 0. Lorsque X du côté droit est 1, X du côté gauche devient 1. En d'autres termes, les compléments doubles redonnent la valeur originale.

Loi commutative

Propriété 14 :

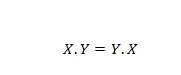
Cela signifie que l'échange du premier et du deuxième opérande pour l'opérateur ET, sur le côté gauche du signe égal, n'a pas d'importance ; la réponse est toujours la même après l'échange du côté gauche. Cette équation peut être écrite en omettant les points sous la forme : XY = YX.

Propriété 15 :

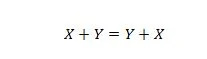
L'explication ici est la même que dans le précédent AND, mais elle concerne l'opérateur OR.

Loi distributive

Propriété 16 :

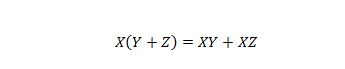
Ici, il y a trois variables : X, Y et Z. Chaque variable peut être 1 ou 0. Sur le côté gauche du symbole égal, les parenthèses signifient d'abord évaluer ce qu'elles contiennent. Ensuite, AND est le résultat avec X. Le côté droit dit que les X ET Y ensemble, OU les X ET Z ensemble, sont identiques au côté gauche. Notez que l'opérateur point pour les ET est omis partout ; et les variables jointes signifient toujours ET.

Propriété 17 :

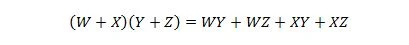
Cette propriété est une extension de la propriété 16 avec la variable ajoutée W.

Droit associatif

Propriété 18 :

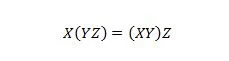
Les parenthèses signifient évaluer en premier ce qui est entre parenthèses. Ainsi, pour l'expression du côté gauche, si Y avec Z sont d'abord associés à AND et X est associé à AND avec le résultat, alors ce résultat final sur le côté gauche est le même que le résultat final sur la droite. -côté main où X avec Y est d'abord ET avant d'effectuer ET le résultat avec Z. Notez que les points ont été omis dans l'équation.

Propriété 19 :

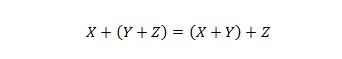
Cette propriété est expliquée de la même manière que la propriété 18, mais l'opérateur OR est utilisé à la place de l'opérateur AND. L'opérateur OR + n'est jamais omis d'une expression booléenne par souci de simplicité. En revanche, l'opérateur AND peut être omis et les deux variables peuvent être jointes.

Absorption

Propriété 20 :

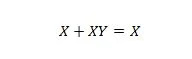
Avec cette équation, quelle que soit la valeur de Y, le membre de droite sera toujours X (absorbé).

Propriété 21 :

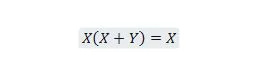
De plus, avec cette équation, quelle que soit la valeur de Y, le membre de droite sera toujours X (absorbé). Cette propriété 21 est la même que la propriété 20 qui est :

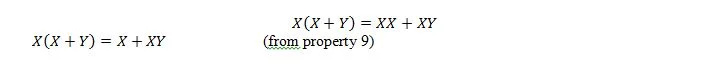
Ici, nous utilisons la loi distributive et le fait que X.X = X de la propriété 9.

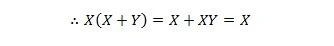
Une identité

Propriété 22 :

Cela signifie que pour l'expression X + Y, le complément de X devant Y ne change pas l'expression.

Propriété 23 :

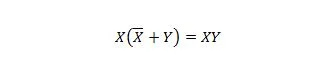
Cela signifie que pour l'expression XY, le complément de X ORed avec Y entre parenthèses, qui est effectué en premier, ne modifie pas l'expression XY.

La loi de DeMorgan

Propriété 24 :

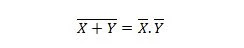
Cela signifie qu'une porte NOR (NOT OR) a le même résultat que de NOTer les deux entrées avant de les associer à AND.

Propriété 25 :

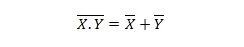
Cela signifie qu'une porte NAND (NOT AND) a le même résultat que de NOTer les deux entrées avant de faire un OU.

Les illustrations fournies sont les 25 propriétés. Ils peuvent être prouvés en substituant toutes les différentes valeurs possibles de 1 et de 0, dans chaque expression du côté gauche, pour voir si l’expression (ou le résultat) du côté droit est obtenu. Les épreuves sont laissées en exercice au lecteur.

2.5 Simplification des expressions composées

Les deux fonctions suivantes sont identiques :

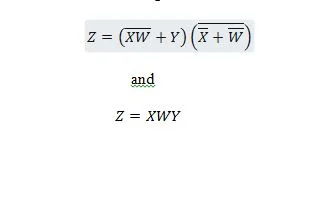
Z est la sortie et X, W et Y sont les entrées. Le premier nécessite une porte NAND, une porte OU, une porte ET, deux portes NON, une porte OU et une porte NON-OU. La seconde n’a besoin que de deux portes ET. La première est une équation avec une expression composée, sur le côté droit, qui a été simplifiée (réduite) au seul terme d'expression de droite pour la deuxième équation.

La simplification ou la réduction conduit à moins de portes afin de mettre en œuvre la même fonction qu'un circuit. Un tel circuit plus petit peut faire partie d'un circuit intégré (CI) ou être un circuit autonome sur la surface de la carte mère de l'ordinateur.

Lorsqu'une fonction (équation) arrive au processus de conception, une simplification doit avoir lieu pour réduire le nombre de portes et aboutir à un circuit moins cher. La simplification nécessite l'emploi d'une ou plusieurs des vingt-cinq propriétés booléennes précédentes.

Exemple 2.51 :

Réduisez l’équation :

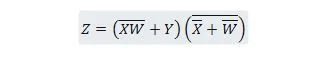
Note: Deux parenthèses côte à côte signifient que les parenthèses sont associées à un AND (le point entre elles n'a éventuellement pas été écrit).

Solution:
Pour les solutions, la justification (raison) de chaque étape est donnée à droite de l’étape, entre parenthèses. Le lecteur doit lire chaque étape et sa justification. Le lecteur doit également se référer aux propriétés précédentes lorsqu'il lit les étapes de réduction de fonction.

Exemple 2.52 :

Simplifier:

2.6 Somme minimale de produits

Les deux fonctions suivantes sont identiques :

Les deux expressions de droite des deux équations sont dites sous la forme Somme des produits (SP). Une expression expresse est dite sous la forme Somme du produit si elle ne comporte pas de parenthèses. Il est évident que la première fonction (équation) nécessite plus de portes que la seconde fonction.

La première expression de droite peut encore être réduite pour obtenir la deuxième fonction. La deuxième expression de droite ne peut pas être simplifiée davantage et reste exprimée comme la somme des produits (« addition » de termes). La deuxième expression de droite ne peut pas vraiment être simplifiée davantage. On dit donc qu'il se présente sous la forme de la somme minimale de produits (MSP).

Exemple 2.61 :
Apportez d’abord la fonction suivante au formulaire Somme des produits, puis au formulaire Somme minimale des produits.

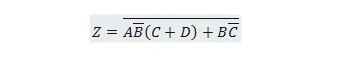
Solution:
Lors de la résolution de problèmes comme celui-ci, une ou plusieurs des vingt-cinq propriétés précédentes doivent être utilisées comme illustré dans cette solution :

2.6 Somme minimale de produits

Les deux fonctions suivantes sont identiques :

Les deux expressions de droite des deux équations sont dites sous la forme Somme des produits (SP). Une expression expresse est dite sous la forme Somme du produit si elle ne comporte pas de parenthèses. Il est évident que la première fonction (équation) nécessite plus de portes que la seconde fonction.

La première expression de droite peut encore être réduite pour obtenir la deuxième fonction. La deuxième expression de droite ne peut pas être simplifiée davantage et reste exprimée comme la somme des produits (« addition » de termes). La deuxième expression de droite ne peut pas vraiment être simplifiée davantage. On dit donc qu'il se présente sous la forme de la somme minimale de produits (MSP).

Exemple 2.61 :
Apportez d’abord la fonction suivante au formulaire Somme des produits, puis au formulaire Somme minimale des produits.

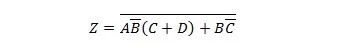
Solution:
Lors de la résolution de problèmes comme celui-ci, une ou plusieurs des vingt-cinq propriétés précédentes doivent être utilisées comme illustré dans cette solution :

Cette dernière expression est sous la forme Somme des produits (SP), mais pas sous la forme Somme minimale des produits (MSP). La première partie de la question a reçu une réponse. La solution pour la deuxième partie est la suivante :

Cette dernière fonction simplifiée (équation) est sous forme MSP et nécessite moins de portes pour sa mise en œuvre que sa forme SP correspondante. N'oubliez pas : SP signifie Somme de produits tandis que MSP signifie Somme minimale de produits.

Exemple 2.62 :
Le circuit suivant a les entrées X, Y et W et Z est la sortie. Produisez la fonction Somme des produits (SP) (fonction de somme minimale apparente des produits) pour Z. Ensuite, produisez la véritable Somme des produits (MSP) plus réduite (minimisée). Ensuite, implémentez le circuit MSP (dessinez le réseau de portes MSP).

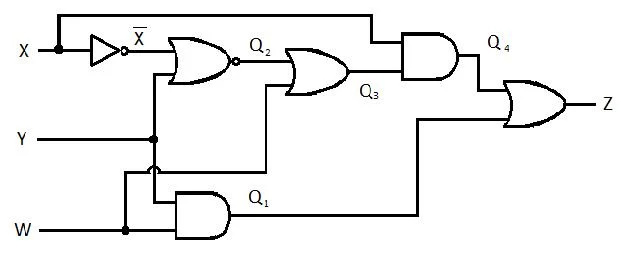
Fig 2.61 Un circuit de déclenchement

Solution:
Avant de commencer le processus de simplification, l'expression de Z doit être obtenue en termes de X, Y et W. Reportez-vous à cet exemple d'illustration tiré du diagramme :

Il s'agit de l'expression de Z en termes de X, Y et W. Après cela, la simplification en MSP apparent peut avoir lieu. Le MSP apparent est SP.

Cette dernière équation (fonction) est sous forme SP. Ce n'est pas la vraie somme minimale de produits (pas encore MSP). La réduction (minimisation) doit donc se poursuivre.

Cette dernière équation (fonction) est une véritable somme minimale de produits (MSP). Et le circuit de déclenchement de la somme minimale des produits (véritable minimisation) est :

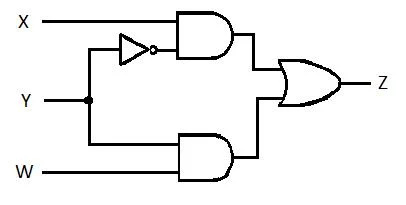
Fig 2.62 Circuit de déclenchement MSP

Commentaire
De l'analyse de cette section, il ressort qu'il n'est pas clair si la somme des produits est la somme minimale des produits ou non. SP n'est pas très utile. C'est MSP qui est très utile. Il existe un moyen assuré d’obtenir MSP ; il s'agit d'utiliser la carte Karnaugh. Karnaugh Map dépasse le cadre de ce cours de carrière en ligne.

2.7 Problèmes

Il est conseillé au lecteur de résoudre tous les problèmes d'un chapitre avant de passer au chapitre suivant.

1. Produisez les tables de vérité ET, OU et NON avec leurs portes correspondantes.
2. Notez les dix postulats booléens dans leurs différentes catégories, en nommant les catégories.
3. Sans explication, notez les vingt-six propriétés de l'algèbre booléenne dans leurs différentes catégories, en nommant les catégories.
4. Réduisez l'équation en utilisant les propriétés booléennes et en citant les catégories utilisées.



5. Réduisez l'équation en utilisant les propriétés booléennes et en citant les catégories utilisées.



6. En utilisant les propriétés booléennes et en citant les catégories utilisées, réduisez l'équation suivante – d'abord à la somme des produits, puis à la somme minimale des produits :



7. En utilisant les propriétés booléennes et en citant les catégories utilisées, réduisez l'équation suivante – d'abord à la somme des produits, puis à la somme minimale des produits :